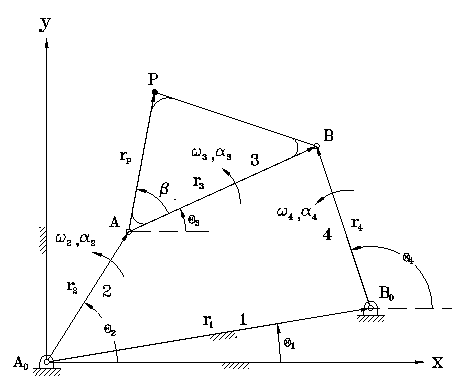
Interactive Four-Bar Linkage Angular Acceleration Analysis

Acceleration analysis begins with formulating the loop-closure equation for the fourbar mechanism shown below. 

r2+r3=r1+r4	    (1)
Taking two derivatives of the above relation, we obtain the acceleration relation 
i*alpha3*r3*exp(i*theta3)-omega3^2*r3*exp(i*theta3)-i*alpha4*r4*exp(i*theta4)

+omega4^2*r4*exp(i*theta4) = i*alpha2*r2*exp(i*theta2)+omega2^2*r2*exp(i*theta2)	(2)
To derive analytical solutions for alpha3 and alpha4 we will assume the link lengths (r1,r2,r3,r4), the angular positions (theta1, theta2, theta3, theta4), the angular velocities (omega1, omega2, omega3, omega4) and at least one angular acceleration is known.

After multiplying (2) by exp(-i*theta4), taking the real part and simplifying, we get 

alpha3=(-r2*alpha2*sin(theta4-theta2)+r2*omega2^2*cos(theta4-theta2)

+r3*omega3^2*cos(theta4-theta3)-r4*omega4^2)/r3*sin(theta4-theta3)      (3)
Similarly the following formula for alpha4 can be derived by multiplying (2) by exp(-i*theta3), 
alpha4=(r2*alpha2*sin(theta3-theta2)-r2*omega2^2*cos(theta3-theta2)

+r4*omega4^2*cos(theta3-theta4)-r3*omega3^2)/r4*sin(theta3-theta4)      (4)
Please note the same methodology can be used to derive formulas for alpha2 and alpha4 given alpha3, and formulas for alpha2 and alpha3 given alpha4.

The interface below allows the user to find the two unknown angular accelerations given the link lengths, theta1, one additional position, one angular velocity, and one angular acceleration.


Unit Type:
Link lengths (m or ft): r1: r2: r3: r4: rp:
Mode for all angles: theta1: beta:

Select and input the known angle (theta2, theta3, or theta4):
value:

Select and input the known angular velocity (omega2, omega3, or omega4):
value:

Select and input the known angular acceleration (alpha2, alpha3, or alpha4):
value:

Powered by Ch