Interactive Four-Bar Linkage Angular Velocity Analysis

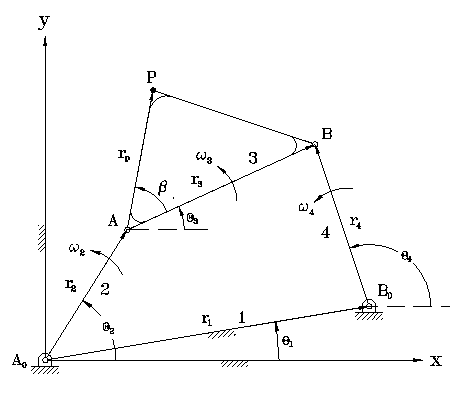Velocity analysis begins with formulating the loop-closure equation for the fourbar mechanism shown below. 
r2+r3=r1+r4	    (1)
Taking the derivative of the above relation, we obtain the velocity relation 
omega3*r3*exp(i*theta3)-omega4*r4*exp(i*theta4)=-omega2*r2*exp(i*theta2)	(2)
To derive analytical solutions for omega3 and omega4 we will assume the link lengths (r1,r2,r3,r4), the angular positions (theta1, theta2, theta3, theta4), and the angular velocity of link 2 (omega2) is known.

Multiplying (2) by exp(-i*theta4) and taking the imaginary part we get 

omega3*r3*sin(theta3-theta4)=-omega2*r2*sin(theta2-theta4)      (3)
and after simplifying 
omega3=-omega2*r2*sin(theta4-theta2)/(r3*sin(theta4-theta3))       (4)
Similarly the following formula for omega4 can be derived by multiplying (2) by exp(-i*theta3), 
omega4=omega2*r2*sin(theta3-theta2)/(r4*sin(theta3-theta4))       (5)
Please note the same methodology can be used to derive formulas for omega2 and omega4 given omega3, and formulas for omega2 and omega3 given omega4.

The interface below allows the user to find the two unknown angular velocities given the link lengths, theta1, one additional position and one angular velocity.


Unit Type:
Link lengths (m or ft): r1: r2: r3: r4: rp:
Mode for all angles: theta1: beta:

Select and input the known angle (theta2, theta3, or theta4):
value:

Select and input the known angular velocity (omega2, omega3, or omega4):
value:

Powered by Ch